Het basismodel
Dit artikel gaat over de uitwerking van Steve Keen’s endogeen geld model zoals beschreven in zijn artikel Solving the paradox of monetary profits. Dit model heeft samen met zijn Extended Goodwin model de basis gevormd voor zijn Monetaire Minsky model.
Keen heeft het model endogeen geld model genoemd omdat een belangrijk uitgangspunt van het model is dat niet de overheid maar de banken de geldhoeveelheid bepalen (zie het artikel Endogeen of exogeen?). Het model kent alleen kredietgeld, geen fiatgeld en geen Centrale bank.
Het is in eerste aanleg een puur monetair model, dat stapsgewijs wordt uitgewerkt:
- in de eerste stap wordt uitgegaan van een vaste hoeveelheid geld in omloop;
- in de tweede stap wordt gestart met diezelfde hoeveelheid geld, maar wordt dat bedrag vervolgens met een bepaald percentage per jaar verhoogd (endogene geldgroei);
- in de derde stap wordt het monetaire model gekoppeld aan een model van de fysieke economie (de productie van - en handel in goederen en diensten) en worden beide modellen gekoppeld via een Phillips vergelijking;
- in de vierde stap wordt een kredietcrisis gesimuleerd.
Het voorgaande klinkt misschien wat afschrikwekkend, maar zoals je hierna zult zien is het eigenlijk heel simpel.
De spelers
Het model kent drie spelers:
- bank
- bedrijven
- werkers (huishoudens)
De geldstromen
In het model worden de volgende geldstromen onderscheiden:
- de bank (Ba) leent geld aan de bedrijven (Be)
- de bedrijven betalen rente aan de bank (rente op lening)
- de bank betaalt rente aan de bedrijven (rente op saldo)
- de bedrijven betalen loon aan de werkers (We)
- de bank betaalt rente aan de werkers (rente op saldo)
- de werkers kopen producten van de bedrijven (consumptie)
- de bankiers kopen producten van de bedrijven (consumptie)
- de bedrijven lossen hun leningen aan de bank af
NB. in deze geldstromen zitten de belangrijkste elementen van een economie, hoewel sommige niet expliciet worden gemaakt:
- bedrijven lenen geld van de bank om hun activiteiten op te starten en uit te voeren (expliciet gemaakt);
- bedrijven investeren geld in gebouwen, machines en grondstoffen (niet expliciet gemaakt, omdat ze die van andere bedrijven kopen, het is dus een geldstroom binnen de sector Bedrijven);
- bedrijven huren werkers in (loon, expliciet gemaakt);
- bedrijven verkopen hun producten aan werkers en bankiers (expliciet gemaakt) en aan elkaar (niet expliciet gemaakt want het is een geldstroom binnen de sector bedrijven);
- bedrijven betalen de bank rente en aflossing over hun lening (expliciet gemaakt);
- bedrijven en werkers ontvangen van de bank rente over het saldo op hun rekening (expliciet gemaakt).
NB. natuurlijk missen er ook elementen. Zo is er geen overheid die de geldstromen kan sturen via belastingheffing en overheidsuitgaven, de laatste al dan niet mede gedekt met geleend geld of met vers gedrukt geld. Daarnaast zijn er geen investeerders, die kapitaal investeren in ruil voor rendement. Verder wordt ervan uitgegaan dat al het geld in omloop ten goede komt van nieuwe productie, wat niet vanzelfsprekend is. Maar deze elementen kunnen in een later stadium worden toegevoegd. Verder is het een puur monetair model, de wisselwerking met de fysieke economie is impliciet gemaakt.
De geldstromen zijn aangegeven in de volgende bankbalans. Verplichtingen hebben een minteken gekregen zodat bezittingen en verplichtingen altijd tot nul optellen. Dat betekent dat in de posten die vallen onder de verplichtingen plussen minnen zijn geworden en omgekeerd.
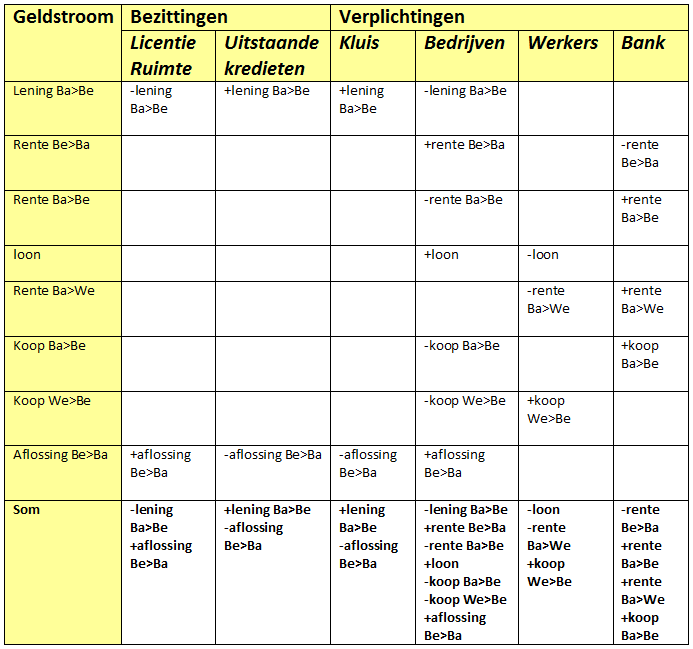
NB. stel je de post “Kluis” voor als een ruimte waarin de bank een geldpers heeft staan waarmee ze naar eigen inzicht geld kan drukken. Omdat in een boekhoudkundige balans echter geen geld uit het niets mag verschijnen is in de balans de post Licentieruimte opgenomen. Dit is een post die de kredietruimte weergeeft die de bank nog heeft.
NB. de post “Bank” betreft het eigen vermogen van de bank, het geld wat van haarzelf is.
NB. stel je voor het gemak voor, net als in het eerder beschreven fictieve monetaire systeem, dat de bank slechts gebruik maakt van een soort bankbiljetten en dat er geen elektronisch geld wordt gebruikt.
De geldstromen nader gespecificeerd
Om het model verder te kunnen uitwerken zijn een aantal constanten nodig. Deze zijn aangegeven in de volgende tabel.

Met verstrekkingtempo leningen wordt bedoeld dat het geld dat in de Kluis zit in een tempo van 3/4 keer de inhoud van de kluis per jaar aan de bedrijven wordt verstrekt als leningen. Met verstrekkingtempo lonen wordt bedoeld dat het geld dat de bedrijven op hun rekeningen hebben staan in een tempo van 2 keer het saldo op die rekeningen per jaar als lonen aan de werkers wordt betaald. Met consumptietempo werkers wordt bedoeld dat het geld dat de werkers op hun rekeningen hebben staan in een tempo van 26 keer het saldo op die rekeningen per jaar door de werkers wordt geconsumeerd (wat correspondeert met het tweewekelijks uitbetalen van de lonen). Met aflostempo leningen tenslotte, wordt bedoeld dat die leningen in een tempo van 1/7 keer de omvang van de uitstaande leningen worden afbetaald (wat correspondeert met een looptijd van de leningen van 7 jaar).
Steve Keen geeft in zijn artikel aan dat de in de tabel aangegeven waarden corresponderen met in de echte wereld gangbare waarden. Overigens kunnen deze waarden naar eigen inzicht worden aangepast.
De modelvergelijkingen
Op basis van de in de eerste tabel aangegeven geldstromen en de in de tweede tabel aangegeven constanten kan het rekenkundige model nu eenvoudig worden uitgeschreven. Dit is hierna aangegeven.
NB. Omdat de geldstromen nu worden berekend vanuit het perspectief van de ontvanger, niet dat van de bank, zijn de tekens onder de verplichtingen in de bankbalans omgedraaid. De minnen zijn dus plussen geworden en omgekeerd.
Δkluis/Δt = - Vlening * Kluis + Vaflossing * Uitstaande kredieten
Δbedrijven/Δt = Vlening * Kluis - Rneg * Uitstaande kredieten + Rpos * Bedrijven - Vloon * Bedrijven
+ Vbcons * Bank + Vwcons * Werkers - Vaflossing * Uitstaande kredieten
Δwerkers/Δt = Vloon * Bedrijven + Rpos * Werkers - Vwcons * Werkers
Δbank/Δt = Rneg * Uitstaande kredieten - Rpos * Bedrijven - Rpos * Werkers - Vbcons * Bank
ΔUitstaande kredieten/Δt = - Δkluis/Δt
NB. Het model van Keen is op een punt niet in lijn met het door hem aangehaalde concept van endogene geldcreatie. Die creatie vindt namelijk plaats op de rekeningen van haar klanten, niet in een denkbeeldige kluis waar het vervolgens driekwart jaar ligt te wachten om te worden uitgeleend. Maar dit punt heeft nauwelijks invloed op de werking van zijn model (zie ook onder MMT).
Het basismodel
Dit model is uitgewerkt in het onderstaande Vensim PLE model. Voor meer informatie over Vensim PLE modellen, zie het artikel over Vensim PLE.
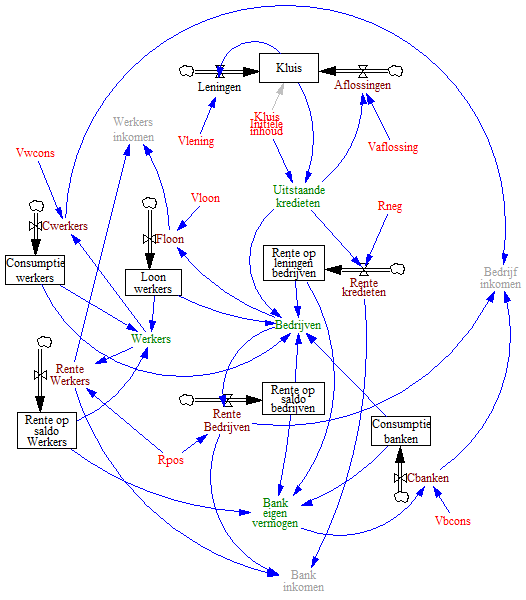
De rode variabelen in dit model zijn de constanten zoals aangegeven in de voorgaande tabel. De bruine variabelen zijn de flow variabelen, corresponderend met de termen in de voorgaande vergelijkingen (bijvoorbeeld: Leningen correspondeert met - Vlening * Kluis). De groene variabelen zijn de stock variabelen. Om praktische redenen zijn deze echter niet als stockvariabelen geprogrammeerd, maar zijn de termen ieder voor zich geïntegreerd, waarna ze in de groene variabelen bij elkaar zijn opgeteld. Het resultaat is hetzelfde.
In het model zijn ook nog grijze variabelen aangegeven. Deze geven de inkomstenstromen aan. Voor de werkers is dat loon plus rente op saldo. Voor de bedrijven is dat inkomsten uit consumptie en rente op saldo. En voor de bank tenslotte zijn dat de netto rente inkomsten. Het model is op de website te downloaden als Endogeen geld model V1.
In de volgende figuur zijn de resultaten te zien van de doorrekening van het model op basis van een kapitaal van 100.000.000 euro. Wat er gebeurt, is dat het kredietgeld gestaag de kluis verlaat en door het systeem gaan stromen. Omdat in het begin al het geld zich nog in de Kluis bevindt en er dus nog niets is uitgeleend, moet zich eerst een evenwicht instellen waarbij het tempo van verlening van nieuwe kredieten even groot is als de aflossing van bestaande kredieten. Te zien valt dat dat na een jaar of 5 het geval is.
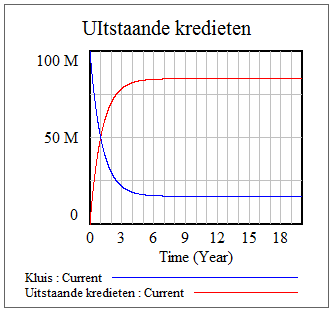
De verstrekte kredieten gaan door het systeem stromen in de vorm van betalingen van loon, rente, consumptie en aflossing. Die stromen vinden plaats via de rekeningen van de bedrijven, de werkers en de bank. Er ontstaat een evenwicht van inkomsten, uitgaven, kredietverlening en afbetaling, waardoor het saldo op de rekeningen en de inkomsten en uitgaven zich na een jaar of 5 stabiliseren. Dat is te zien in de figuur hierna.
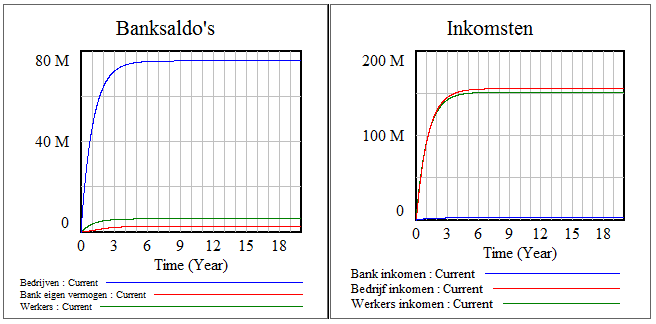
In de rechter grafiek is te zien dat de inkomsten van de werkers en de bedrijven veel hoger zijn dan die van de bank. Dat komt doordat de bank alleen geld verdient aan de kleine marge tussen rente op schuld en rente op banksaldo’s. In de linker grafiek is te zien dat het saldo op de rekening van de bedrijven veel hoger is dan dat op de rekening van de werkers, terwijl hun inkomsten vergelijkbaar zijn. Dat komt doordat de werkers het geld op hun rekening in een veel hoger tempo uitgeven (aan consumptie) dan de bedrijven het saldo op hun rekening uitgeven (aan lonen, rente en aflossing).
Toevoeging van geldgroei
De eerste uitbreiding van het model is de toevoeging van geldgroei, als gevolg van groei van de uitstaande kredieten.
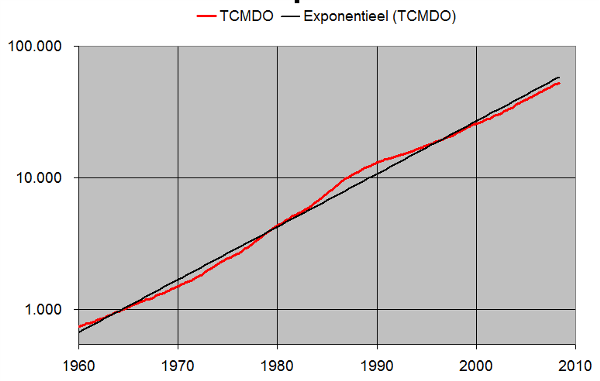
In de onderstaande grafiek is de groei van alle uitstaande kredieten in de VS (huishoudens, bedrijven en overheid) in de periode 1960 - 2008 weergegeven (bron: Amerikaanse Centrale bank). De bedragen zijn in miljarden dollars. De uistaande kredieten zijn in deze periode gegroeid van minder dan 1.000 miljard dollar tot ruim 50.000 miljard dollar.
Ik heb in de grafiek gebruik gemaakt van een logaritmische schaal omdat de uitstaande kredieten in die periode exponentieel gegroeid zijn, wat wil zeggen dat ze met een min of meer constant percentage per jaar zijn gestegen. Een exponentiele groei wordt bij zo'n schaal een min of meer rechte lijn. De rode lijn geeft de omvang van de uitstaande kredieten weer. De zwarte lijn is de best passende lijn met een vast groeipercentage, in dit geval 9,2%.
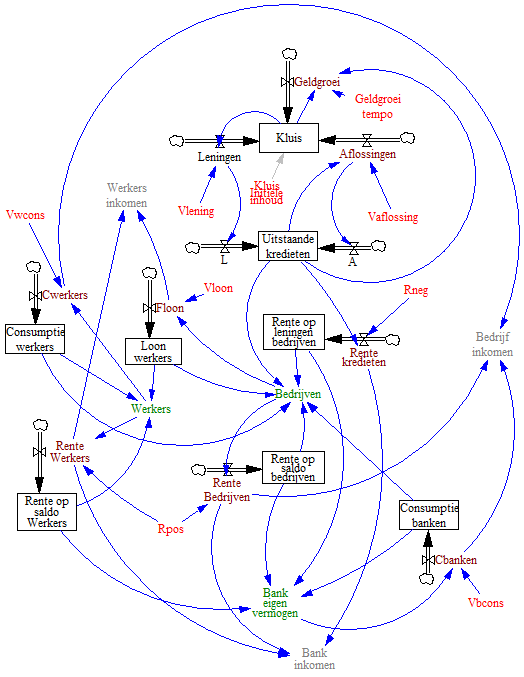
Steven Keen houdt in zijn model een groei van de hoeveelheid geld in omloopmet een fractie 1/15 aan. Dat komt overeen met een jaarlijkse toename van de geldhoeveelheid met 6,7%, beduidend minder dan de in de VS in de periode 1960 - 2008. Het uitgebreide model is hieronder te zien. Aan het model zijn de flow variabele Geldgroei en de constante Geldgroei tempo (=1/15) toegevoegd.
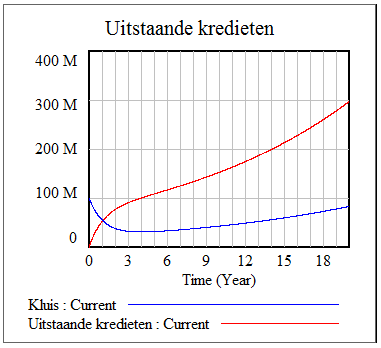
Als gevolg van de geldgroei stelt zich ook nu weer een evenwicht in tussen de hoeveelheid uitstaande kredieten en het saldo in de kluis. Maar ditmaal is dat geen constant niveau maar een situatie waarin beiden in hetzelfde tempo toenemen, namelijk het tempo van de geldgroei, in dit voorbeeld dus 6,7% van de totale hoeveelheid geld. Dat is te zien in de volgende figuur.
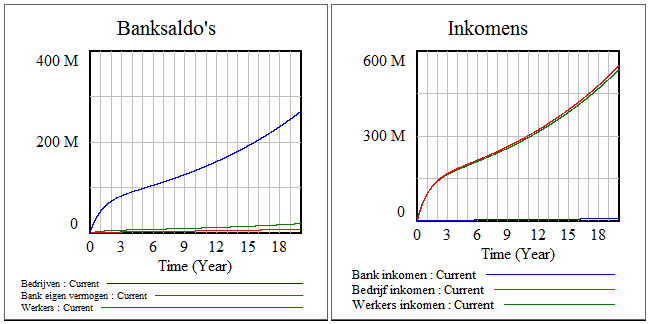
In de figuur hierna is voor de situatie met 6,7% geldgroei de ontwikkeling van de banksaldi en de inkomsten te zien.
In het volgende artikel, Endogeen geld model - II, ga ik nader in op de toevoeging van de fysieke component en de simulering van een kredietcrisis.
© Anton van de Haar - november 2012