In hoofdstuk 8 Tijd, voorraden, winsten en prijsvorming van hun boek Monetary Economics gaan G&L uitgebreid in op een aantal cruciale factoren bij de operaties van bedrijven en van het effect daarvan op de verdeling van de opbrengsten van de productie over werknemers en geldschieters. In het vorige artikel is ingegaan op de eerste drie factoren: tijd, voorraden en winsten. In dit artikel wordt ingegaan op de vierde factor: prijsvorming.
In het vorige artikel was al duidelijk geworden dat de prijsvorming
grote invloed heeft op de winstgevendheid van bedrijven. Maar hoe die prijsvorming
tot stand komt is nog niet aan de orde geweest, dat wordt in dit artikel
behandeld.
Meer concreet willen G&L de vraag beantwoorden: wat proberen bedrijven te bereiken als ze
hun prijzen vaststellen? Vooruitlopend op de beantwoording van die vraag
geven ze alvast een algemeen antwoord: die
bedrijven proberen daarmee voldoende winst te genereren om hun investering in
productiemiddelen te kunnen betalen en bovendien een zodanig dividend uit te kunnen
keren dat ze hun aandeelhouders tevreden kunnen stellen.
Cost-plus pricing
Bij de nadere beantwoording van hun vraag starten G&L
met een simpele veronderstelling, namelijk dat bedrijven proberen om een zekere
winstmarge op hun verkopen te bereiken. De volgende vraag is dan: wat voor een prijs moeten ze vaststellen om
de gewenste marge te kunnen bereiken?
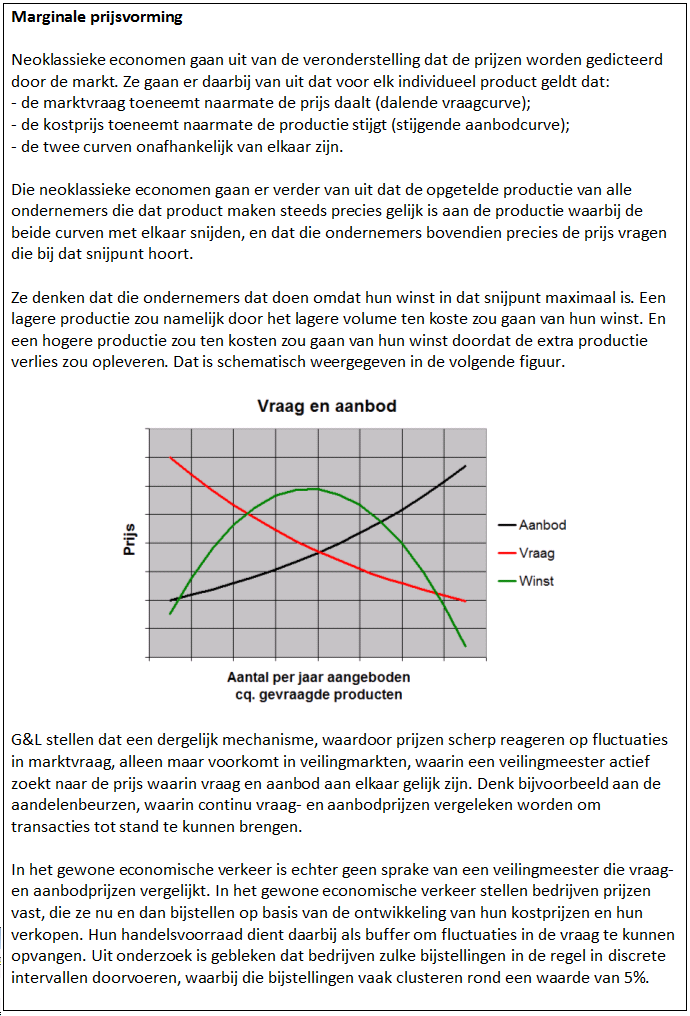
G&L geven aan dat de vaststelling van prijzen in de
regel plaatsvindt op basis van gewoontes en verwachtingen. Bedrijven kijken
naar een zekere maatstaf van hun eenheidkosten, waar ze vervolgens een marge bij
optellen om te komen tot hun verkoopprijzen. Deze benadering wordt aangeduid
met cost-plus pricing.
NB. Het principe van
cost-plus pricing wordt algemeen gevolgd door heterodoxe economen, die het gangbare
neoklassieke principe van marginale prijsvorming afwijzen. Dat laatste principe
heb ik voor de duidelijkheid kort uiteengezet in het volgende kader (eigen toevoeging).
Wel of niet meetellen van de rentekosten in de eenheidskostenberekening
NB. Allereerst een opmerking.
Dit artikel heeft, net als het voorgaande, betrekking op een verticaal
geïntegreerd model van de economie. Daarmee wordt bedoeld dat alle stappen van de
grondstofwinning tot het maken van eindproducten op een hoop gegooid zijn. En
dat betekent dat alle kosten herleid zijn tot loonkosten en winstkosten. Daarom
wordt er alleen gekeken naar investeringen in voorraden, niet naar
investeringen in productiemiddelen.
Voor het aspect
investering in productiemiddelen verwijs ik naar de artikelen over het BMW
model. In hun meest complexe modellen hebben G&L overigens zowel het aspect
investering in productiemiddelen (in de lijn van het BMW model) als het aspect de
investering in voorraden meegenomen.
G&L constateren dat de meeste post-Keynesiaanse economen
ervan uitgaan dat bedrijven bij de kostprijsberekening de rentekosten op
investeringen in voorraden niet meerekenen. Dat betekent dat variaties in de rentestand
niet doorwerken in de verkoopprijzen, maar alleen doorwerken in de winst. Het
gevolg daarvan is dat variaties in de rentestand, omdat de verkoopprijzen
onveranderd blijven, geen effect hebben op de reële lonen.
Een andere benadering, waar G&L zich bij aansluiten, is
dat bedrijven wel degelijk rekening houden met die rentekosten, en dat ze verandering
van die kosten doorberekenen in de verkoopprijzen. Dat betekent dat een
stijging van de rente leidt tot een stijging van de verkoopprijzen. En dat
leidt tot dalende reële lonen, vanwege die stijgende verkoopprijzen.
Cost-plus pricing op z’n simpelst: mark-up pricing
De simpelste benadering van cost-plus pricing is mark-up
pricing. Zoals we in het vorige artikel al zagen, komt ze erop neer dat de
kostprijs met een doelmarge wordt verhoogd:
p = ( 1 + ϕ ) · W / pr = ( 1 + ϕ ) · UC
In de vergelijking staat p voor de verkoopprijs, ϕ voor de doelmarge
(mark-up), W voor de loonkosten per tijdseenheid, pr voor de productie per
tijdseenheid (de arbeidsproductiviteit) en UC voor de kosten per eenheid
product, hier de loonkosten per eenheid product W / pr.
NB. in het vorige
artikel hadden we het over de achteraf berekende winstmarge ϕ’. Nu gaat het
over de van tevoren gekozen doelmarge ϕ.
Laatstgenoemde vergelijking gaat echter voorbij aan het feit
dat een deel van de verkochte producten kan zijn gemaakt in de vorige periode,
tegen andere productiekosten en met rentekosten. Even terug naar het vorige
artikel. Daarin is verondersteld dat van de producten die in de lopende periode
worden verkocht een fractie 1 – σ
is geproduceerd in de lopende periode en een fractie σ in de voorgaande
periode.
Voor die eerste fractie zijn de kosten per eenheid product gelijk
aan de actuele loonkosten per eenheid product. Maar dat geldt niet voor die
tweede fractie, de producten die zijn gemaakt in de vorige periode. Voor die
producten zijn de kosten niet gelijk aan de actuele loonkosten, UC. Ten eerste
zijn ze gemaakt in de vorige periode, tegen loonkosten UC-1 die niet
noodzakelijk gelijk zijn aan de actuele kosten UC. En ten tweede zijn ze uit
voorraad geleverd, wat met rentekosten gepaard gaat.
G&L geven aan dat ze twee opties zien om hiervoor te
corrigeren: normal cost pricing en historic full cost pricing.
Historic full cost pricing
G&L
beginnen met historic full cost pricing. Zoals we in het vorige artikel
zagen kun je UC corrigeren voor variaties in loonkosten per eenheid product en
voor rentekosten, dan vind je HUC, de historische
kosten per eenheid product:
HUC = ( 1 – σ ) · UC
+ ( 1 + rL-1 ) · σ · UC-1
Op basis van deze vergelijking kun je de voorgaande kostprijsvergelijking
herschrijven tot:
p = ( 1 + ϕ ) · HUC
= ( 1 + ϕ ) · ( ( 1 – σ ) · UC + ( 1 + rL-1 ) · σ · UC-1 )
Een consequentie van deze vergelijking is dat de waarde van
HUC pas berekend kan worden aan het einde van de periode, als duidelijk is hoe
groot het aantal verkochte producten s is geworden. Want pas dan kan, op basis
van de vergelijking σ = in-1 / s, van de hoeveelheid verkochte
producten s de fractie σ worden bepaald die gemaakt is in de vorige periode.
Ondernemers die voor de lopende periode hun prijs willen vaststellen,
zullen dus een aanname moeten doen over het aantal producten dat ze in de
lopende periode denken te verkopen, se. Op basis daarvan kunnen ze σe
berekenen, en op basis daarvan HUCe. Het symbool e staat hierbij
voor het feit dat het om een verwachte waarde gaat:
σe = in-1 / se
p = ( 1 + ϕ ) · HUCe
= ( 1 + ϕ ) · ( ( 1 – σe ) · UC + ( 1 + rL-1 ) · σe · UC-1 )
G&L merken op dit punt op dat uit deze benadering volgt
dat prijzen, kosten en winsten op een eenduidige wijze aan elkaar zijn
gekoppeld. Dat betekent dat de doorwerking van kosten op prijzen dan vastligt.
Die laatste conclusie staat haaks op de basisveronderstellingen in de gangbare econometrie,
wat volgens G&L een verklaring biedt voor het feit dat deze methode hier
nooit vaste voet heeft gekregen.
Perverse pricing
De laatste vergelijking heeft een opmerkelijke consequentie,
namelijk dat als de rentecomponent rL-1 groter is dan ΔUC / UC-1,
een daling van de verwachte verkopen leidt tot een stijging van de verkoopprijs. Dat komt doordat (1 + rL-1)
· UC-1 dan groter is dan UC zodat, naarmate de verwachte verkopen
dalen en de fractie σe daardoor groter wordt, de verkoopprijs p
stijgt. Dit effect wordt perverse pricing
genoemd.
Perverse pricing kan optreden in twee omstandigheden. De
eerste is voornoemd scenario. De tweede is, opnieuw onder de voorwaarde dat de rentecomponent
rL-1 groter is dan ΔUC / UC-1, als de verkopen in de
voorgaande periode lager waren dan verwacht, waardoor de voorraden in-1
groter zijn geworden dan verwacht. Daardoor is de fractie σe groter geworden
dan in de voorgaande periode nog werd verwacht, met als gevolg een lagere
verkoopprijs.
Een oplossing voor perverse pricing: normal cost pricing
Een aantrekkelijke benadering om het optreden van perverse
pricing te omzeilen is door bij de vaststelling van de verkoopprijzen niet uit
te gaan van de verwachte ontwikkeling van de fractie verkochte producten uit de
vorige periode, σe, maar van een zeker doelfractie σT,
bijvoorbeeld op basis van de trendmatige ontwikkeling van σ in de afgelopen
perioden:
σT = inT / se
In deze vergelijking staat se voor de in de
lopende periode verwachte verkopen en inT voor de doelomvang van de
voorraden zoals die door de ondernemers bij de planning van de productie wordt
nagestreefd, waarbij inT een zekere fractie van se is,
zodat σT onafhankelijk wordt van variaties is se. Op
basis hiervan kunnen, analoog aan NUC, de normale
historische kosten per eenheid product NHUC worden gedefinieerd:
p = ( 1 + ϕ ) · NHUC
= ( 1 + ϕ ) · ( ( 1 – σT ) · UC + ( 1 + rL-1 ) · σT · UC-1 )
Het nadeel van deze methode is dat de in deze laatste
vergelijking aangegeven doelmarge gedurende langere tijd kan afwijken van zowel
de op basis van de actuele voorraden in-1 en de verwachte verkopen se
te verwachten winstmarge, als van de uiteindelijk gerealiseerde winstmarge.
G&L merken echter op dat bedrijven die dat constateren dit eenvoudig kunnen
bijsturen door hun doelmarge aan te passen.
Het voordeel van deze methode is dat ze ongevoelig is voor
perverse pricing, een meer stabiele prijsontwikkeling genereert en eenvoudig
kan worden toegepast, omdat UC-1, UC en rL-1 eenvoudig
kunnen worden bepaald aan de hand van accountantsgegevens.
NB. G&L merken op
dat in de echte wereld UC niet precies bekend is aan het begin van de periode,
omdat ze tevens afhangt van de ontwikkeling van de arbeidsproductiviteit.
Hiervoor zou kunnen worden gecorrigeerd door een zekere (cyclisch gecorrigeerde)
ontwikkeling van de arbeidsproductiviteit te veronderstellen.
Historic full cost pricing en normal cost pricing nader bezien
Waar komen full cost pricing en normal cost pricing nu
eigenlijk op neer? Dat kan duidelijker gemaakt worden door te veronderstellen
dat UC = UC-1. De algemene kostprijsvergelijking wordt dan:
p = ( 1 + ϕ ) · ( ( 1 – σ ) ·
UC + ( 1 + rL-1 ) · σ · UC )
= ( 1 + ϕ ) · ( UC - σ · UC + σT · UC + rL-1 · σ · UC )
= ( 1 + ϕ ) · ( 1 + rL-1 · σ) · UC
Uit deze vergelijking blijkt heel helder het principe van
cost-plus pricing: de verkoopprijs is gelijk aan de eenheidskosten, verhoogd
met een rentemarge rL-1 · σT ter dekking van de voorraadkosten, en die twee samen
nogmaals verhoogd met een winstmarge.
De voorgaande vergelijking geld alleen als UC = UC-1. Ze kan echter onafhankelijk worden gemaakt van de ontwikkeling van de eenheidskosten UC in de tijd door een kleine aanpassing, namelijk door de nominale rentevoet rL-1 te vervangen door een reële rentevoet. Om dat duidelijk te maken introduceren G&L een nieuwe variabele, kosteninflatie πc:
πc = ( UC – UC-1
) / UC-1
G&L merken op dat πc bijna precies gelijk is
aan de ontwikkeling van de nominale lonen minus de ontwikkeling van de
arbeidsproductiviteit. Ze kan worden herschreven tot:
πc = UC / UC-1
– 1
πc + 1 = UC / UC-1
1 / ( πc + 1 ) = UC-1 / UC
UC-1 = UC / ( πc + 1 )
Op dit punt introduceren G&L een volgende nieuwe
variabele, de reële rente op basis van kosteninflatie rrc. Deze
wordt veelal gedefinieerd als rrc = rL- πc, maar dat is slechts een
benadering.
De correcte vergelijking voor rrc kan als volgt
worden afgeleid. Stel, je hebt een monetair bezit waarvan de waarde aan het
begin van de vorige periode M-1 bedroeg. In het begin van de huidige
periode is die waarde door rentebetaling toegenomen tot M-1 · ( 1 +
rL-1). De reële waarde na correctie van kosteninflatie bedraagt dan
M-1 · ( 1 + rL-1) / ( 1 + πc ). Op basis
daarvan is de waarde van de ontvangen rente na kosteninflatie gelijk aan:
M-1 · ( 1 + rL-1) / ( 1 + πc ) – M-1
De reële rentevoet rrc-1 bedraagt dan:
rrc-1 = ( M-1 · ( 1 + rL-1) / ( 1 + πc ) – M-1 ) / M-1
= ( 1 + rL-1) / ( 1 + πc ) – 1
Zodat:
rrc-1 = ( 1 + rL-1) / ( 1 + πc ) – 1
1 + rrc-1 = ( 1 + rL-1) / ( 1 + πc )
( 1 + rL-1) = ( 1 + rrc-1 ) · ( 1 + πc )
Terug naar de historic
full cost pricing vergelijking eerder in dit artikel:
p = ( 1 + ϕ ) · HUCe
= ( 1 + ϕ ) · ( ( 1 – σe ) · UC + ( 1 + rL-1 ) · σe · UC-1 )
Door in deze vergelijking ( 1 + rL-1 ) te
vervangen door ( 1 + rrc-1 ) · ( 1 + πc ) en UC-1
te vervangen door UC / ( πc + 1 ) vinden we:
p = ( 1 + ϕ ) · ( ( 1 – σe
) · UC + ( 1 + rrc-1 ) · ( 1 + πc ) · σe · UC / ( πc
+ 1 ))
= ( 1 + ϕ ) · ( ( 1 – σe ) · UC + ( 1 + rrc-1 ) · σe · UC )
= ( 1 + ϕ ) · ( 1 + rrc-1 · σe ) · UC
En op precies dezelfde wijze vinden we voor normal cost pricing:
p = ( 1 + ϕ ) · ( 1 + rrc-1
· σT ) · UC
En daarmee hebben we de gezochte kosteninflatie
onafhankelijke vergelijkingen voor de verkoopprijs p op basis van historic full
cost pricing en normal cost pricing gevonden. Ze zijn van belang omdat eruit
blijkt dat de marge over de actuele eenheidskosten UC niet afhankelijk is van de
nominale rente, maar van de reële rente.
Kostprijsinflatie versus verkoopprijsinflatie
Even terug naar de laatste twee vergelijkingen. Als je deze
deelt door p en vermenigvuldigt met de reële productie y, dan vind je (op basis
van de laatste vergelijking als voorbeeld):
p · y / p = ( 1 + ϕ
) · ( 1 + rrc-1 · σT
) · UC· y / p
y = ( 1 + ϕ ) · ( 1 + rrc-1 · σT ) · UC· y / p
Bedenk bij die laatste vergelijking dat UC, de kosten per
eenheid product, gelijk is aan de loonsom WB gedeeld door de reële productie:
WB / y:
y = ( 1 + ϕ
) · ( 1 + rrc-1 · σT
) · ( WB / y ) · y / p
= ( 1 + ϕ ) · ( 1 + rrc-1 · σT ) · WB / p
Als we vervolgens wb definiëren als de reële loonsom WB / p,
dan krijgen we tenslotte:
y = ( 1 + ϕ ) · ( 1 + rrc-1
· σT ) · wb
G&L stellen over deze vergelijking dat het een
fundamentele gedragsvergelijking betreft, die aangeeft dat als bedrijven
prijzen vaststellen, dat ze daarmee per saldo de verdeling van het nationale
inkomen over arbeidsverschaffers, ondernemers en kapitaalverschaffers
bewerkstelligen. Daarin is:
wb / y het
aandeel van de werknemers
rrc-1
· σT · wb / y het
aandeel van de kapitaalverschaffers
ϕ · (
1 + rrc-1 · σT ) · wb / y = ϕ / ( 1 + ϕ ) het aandeel van
de ondernemers
G&L merken op dat zodra twee van deze drie aandelen
vastliggen, het derde aandeel eveneens vastligt. De fundamentele consequentie
daarvan is dat als de ondernemers in staat zijn om hun winstmarge ϕ vast te leggen en de
kapitaalverschaffers in staat zijn om hun reële rentemarge rrc-1
vast te leggen, dat er dan geen ruimte meer is voor de werknemers om hun reële
loon wb vast te leggen.
NB. de voorgaande
vergelijkingen gelden voor normal cost pricing. De vergelijkingen voor historic
full cost pricing kunnen eenvoudig worden verkregen door in de vergelijkingen
σT te vervangen door σe.
In het volgende artikel worden twee rekenvoorbeelden gegeven om de voorgaande theorie wat duidelijker te maken.
© Anton van de Haar - oktober 2013