Antons economie pagina

In hoofdstuk 8, Tijd, voorraden, winsten en prijsvorming, van hun boek Monetary Economics gaan G&L uitgebreid in op een aantal cruciale factoren bij de operaties van bedrijven en van het effect daarvan op de verdeling van de opbrengsten van de productie over werknemers en geldschieters. In dit artikel wordt ingegaan op de eerste drie, tijd voorraden en winsten.

De factor tijd: voorraadvorming

Één van die cruciale factoren is de factor tijd. Omdat er tijd verstrijkt tussen het inzetten van de productie en de uiteindelijke verkoop van de daaruit voortkomende producten, gaan de kosten voor de baten uit. Concreet betekent dit dat er geïnvesteerd moet worden in voorraadvorming. G&L onderscheiden drie oorzaken van voorraadvorming:

1. omdat de productie tijd vergt, hebben bedrijven in de productiefase in de regel te maken met voorraden aan producten in verschillende stadia van gereedheid;
   
2. omdat de distributie van de producten tijd vergt, is er in de distributiefase sprake van een voorraad aan gereed product;
   
3. omdat de vraag naar producten fluctueert, houden bedrijven in de verkoopfase in de regel een buffervoorraad aan om te kunnen reageren op vraagpieken.
   

Over die derde oorzaak merken G&L op dat ook bedrijven die op bestelling produceren uit concurrentieoverwegingen meestal voorraden aanhouden, om snel te kunnen reageren op vraag uit de markt, zodat orders om die reden niet aan hun neus voorbij gaan. Al met al spelen voorraadvorming en de financiering daarvan een cruciale rol bij de operaties van bedrijven.

Het meten van winst

G&L merken op dat in mainstream economische modellen in de regel wordt verondersteld dat de bedrijfswinsten gelijk zijn aan het marginale product van de productiemiddelen maal de waarde van de voorraad productiemiddelen, in jargon: het marginale product van kapitaal maal de kapitaalvoorraad. Dat is echter niet in overeenstemming met wat er in de echte wereld gebeurt.

In de echte wereld weten bedrijven niet op voorhand wat hun productiekosten zullen zijn en hoeveel winst ze daarop kunnen maken. Bij de vaststelling van hun prijzen moeten ze daarom sturen op hun verwachtingen daarover. Pas achteraf zullen ze kunnen vaststellen hoe hoog die productiekosten daadwerkelijk zijn geweest, en op basis daarvan, hoeveel winst ze echt hebben gemaakt.

NB. in dit artikel wordt niet ingegaan op een ander belangrijk aspect van de bepaling van de totale productiekosten, namelijk de kosten van de gebruikte productiemiddelen. Dat aspect wordt in de artikelen over het BMW model behandeld. Het is hier weggelaten omdat G&L uitgaan van een verticaal geintegreerd model, wat wil zeggen dat voor de economie als geheel de kosten van alle producten kunnen worden herleid tot productiekosten en winstkosten.

In de volgende tekst wordt uiteengezet hoe G&L hier tegenaan kijken. Hun benadering sluit aan bij hoe de bedrijven dat zelf ook doen. In de tabel hierna is als voorbeeld een stukje getoond uit een TSM die de operaties toont van de bedrijven die voorraden aanhouden. Om de zaken in dit stadium overzichtelijk te houden is verondersteld dat die bedrijven alle gemaakte winst uitbetalen aan hun aandeelhouders.

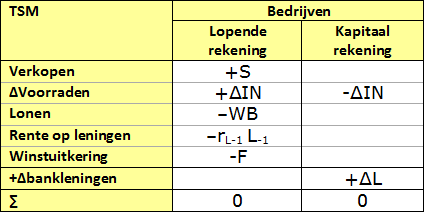
Wat je ziet is dat de bedrijven inkomsten op hun lopende rekening hebben uit de verkoop van hun producten en dat ze al die inkomsten uitgeven aan lonen, rente en winstuitkering. Wat je ook ziet is dat extra voorraadvorming in de huidige periode op de lopende rekening wordt geboekt als bron van inkomsten, +ΔIN, en op de kapitaalrekening als bestemming van uitgaven, –ΔIN. Dat doet mogelijk wat vreemd aan, maar is het niet. Dat zit zo.

Voorraadvorming vergt, zoals hiervoor uiteengezet, een voorinvestering. Die is nodig om de lonen te betalen van de werknemers die de voorraad produceren. In het voorbeeld is verondersteld dat die voorinvestering wordt gefinancierd met geleend geld. Dat gebeurt via de kapitaalrekening, waar +ΔL staat voor de extra lening en –ΔIN voor de overboeking van het zo geleende geld naar de lopende rekening.

Per saldo komt de voorgaande benadering neer op een boekhoudkundige operatie, waarin de productie- en verkoopafdeling van het bedrijf, die de lopende rekening gebruikt, de voorraad aan ongereed product, gereed product in distributiefase en gereed product in de verkoopfase op papier heeft verkocht aan de financieringsafdeling van het bedrijf, die de kapitaalrekening gebruikt en darmee het werkkapitaal beheert.

NB. Zo’n voorinvestering zou natuurlijk ook kunnen worden betaald  uit eigen geld. Vervang in gedachten de regel +Δbankleningen door –Δbanksaldo en de regel Rente op leningen door de regel Rente op banksaldo. Het netto effect is dat voorraadvorming dan niet leidt tot een toename van het leensaldo en de uitgavenpost Rente op leningen, maar een afname van het banksaldo en van de inkomstenpost Rente op banksaldo. Het netto resultaat is vergelijkbaar.

NB. Het model dat weerspiegeld wordt in de TSM gaat voorbij aan het feit dat productie meestal een keten is van producenten met hun eigen tussenproducten en hun eigen winstdoelstelling, dus dat extra voorraadvorming niet alleen wordt weerspiegeld in extra loonkosten, maar ook in extra voorraadvorming aan- en gebruik van grondstoffen en producten van derden. Uit het oogpunt van simpelheid negeren G&L dit vooralsnog.

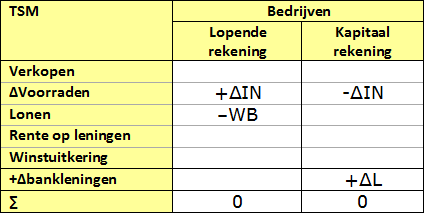
Één van de zaken die volgt uit de voorgaande tabel, is dat een voorraad moet worden gewaardeerd op haar productiekosten, omdat dat de kosten zijn die de productie feitelijk heeft gevergd. Dat blijkt het duidelijkst als wordt verondersteld dat het bedrijf net is opgestart, zodat S, r_L-1 · L_-1 en F nog gelijk zijn aan nul. Op dat moment ziet de TSM van het bedrijf er nog als volgt uit:

De ondernemingswinst F en de brutowinst F_T

Verder met de eerste tabel. Je kunt uit de tweede kolom de volgende vergelijking aflezen:

            F = S + ΔIN – WB – r_L-1 · L_-1

En omdat in het voorbeeld is verondersteld dat de bedrijven alleen lenen om de productie van hun voorraden te financieren en die voorraden op productiekosten worden gewaardeerd, zodat steeds geldt dat L = IN, kun je deze vergelijking herschrijven tot:

            F = S + ΔIN – WB – r_L-1 · IN_-1

Anders gezegd, de winst F die de bedrijven in het voorbeeld maken en waarvan is verondersteld dat ze die uitkeren aan hun aandeelhouders, is gelijk aan de verkopen S plus de verandering van de voorraad ΔIN minus de lonen WB en minus de rentekosten r_L-1 · L_-1.

G&L geven aan dat deze definitie, die ze de ondernemingswinst noemen, hun geprefereerde definitie is van de bedrijfswinst, omdat ze overeenkomt met de hoeveelheid geld die kan worden onttrokken aan een bedrijf zonder de balans van de bezittingen de verplichtingen van dat bedrijf te veranderen. G&L melden in een later stadium te zullen argumenteren dat dit tevens het getal is waar de bedrijven naar kijken als ze hun prijzen vaststellen, waarbij ze uitgaan van een zekere, door hen gewenste winstmarge.

NB. Je zou geneigd kunnen zijn om uit de voorgaande vergelijking op te maken dat vergroting van de voorraad bijdraagt aan de winst. Dat is echter niet zo, omdat de voorraad is geboekt tegen haar productiekosten (loonkosten), zodat het besluit om in een bepaalde periode extra voorraad op te bouwen leidt tot een precies even grote stijging van de loonkosten in die periode, zodat beiden elkaar steeds opheffen. Om dat inzichtelijk te maken is het handiger om de voorgaande vergelijking als volgt te schrijven:

            F = S – ( WB – ΔIN ) – r_L-1 · IN_-1

In aanvulling op deze vergelijking introduceren G&L nog een tweede winstvergelijking, die van de winst voor aftrek van rentekosten, die ze als bruto winst (F_T) aanduiden:

            F_T = S – ( WB – ΔIN )

 

Het meten van de winst nader bezien: het effect van prijsveranderingen

Bij de berekening van de winst met de voorgaande vergelijking treedt een complicatie op, namelijk dat de verandering van de waarde van de voorraad ΔIN deels het gevolg kan zijn is van een herwaardering van de waarde van de voorraad uit de voorgaande periode, als gevolg van een verandering van de prijs van de betreffende producten.

NB. G&L hebben in hun redenering gemakshalve aangenomen (maar niet erg duidelijk benadrukt) dat de tijd tussen de start van de productie en de verkoop van de producten nooit langer dan 1 periode duurt. Dat betekent dat een deel van de op enig moment verkochte producten in de vorige periode is geproduceerd, maar dat er geen producten worden verkocht die in nog eerdere perioden zijn geproduceerd. Dit impliceert tevens dat er wordt uitgegaan van het FIFO principe, First in, First out.

Terug naar voornoemde complicatie. Allereerst introduceren G&L twee nieuwe begrippen, historische loonkosten (HWC) en totale historische kosten (THC):

            HWC = ( WB – ΔIN )

            THC = ( WB – ΔIN ) + r_L-1 · IN_-1

Als je terugkijkt naar de definitie van de ondernemingswinst F en de bruto winst F_T, dan zie je dat THC het verschil is tussen de verkoopopbrengsten S en de ondernemingswinst F en dat HWC het verschil is tussen de S en de bruto winst F_T. Waarom introduceren G&L deze begrippen? Dat zal hierna duidelijk worden.

Fysiek en monetair

G&L maken eerst een zijsprong naar de relatie tussen fysieke en monetaire variabelen. Daarbij introduceren ze de notatie dat fysieke variabelen (uitgedrukt in aantallen producten) met kleine letters worden aangegeven en nominale variabelen (uitgedrukt in geld) met hoofdletters.

Stel je een economie voor waarin alleen maar appels worden geproduceerd, die allemaal exact hetzelfde zijn en waarvan een voorraad wordt aangehouden. De verandering van de voorraad appels in de lopende periode is dan gelijk aan:

            Δin = in – in_-1 = y – s

In deze vergelijking staat y voor de hoeveelheid in de lopende periode geproduceerde appels en s voor de hoeveelheid in die periode verkochte appels. Wat er na de verkoop nog overblijft, y – s, wordt toegevoegd aan de voorraad: Δin.

Vervolgens definiëren G&L unit costs (UC), dat is de prijs per eenheid product, in dit geval dus de prijs per appel. Er geldt:

   IN = in · UC

            UC = WB / y

Op basis hiervan geldt:

            ΔIN = IN – IN_-1 = in · UC – in_-1 · UC_-1

Veranderende prijzen

In de voorgaande vergelijking is het element prijsverandering geïntroduceerd. Dat zagen we eerder al in het artikel Het G&L LP model - I onder het kopje Veranderende bondprijzen. Zoals in dat stukje werd uiteengezet kan de vorige vergelijking worden herschreven tot:

            ΔIN = in · UC – in_-1 · UC_-1

         = in · UC – ( in – Δin) · ( UC – ΔUC)

                  = in · UC – ( in · UC – in · ΔUC – Δin · UC + Δin · ΔUC

                  = in · ΔUC + Δin · UC – Δin · ΔUC

                  = in · ΔUC + Δin · UC_-1

            ΔIN = Δin · UC + ΔUC · in_-1

Deze afleiding, waarmee ΔIN voor het betreffende product is opgesplitst in een factor voor de verandering van de fysieke voorraad en een factor voor de verandering van de eenheidsprijs, kan ook simpel worden afgelezen uit het volgende plaatje. Uit het plaatje kun je ook afleiden dat de laatste twee stappen in de voorgaande afleiding identiek zijn: trek het beige blok door omlaag, over het gele blok heen, en je hebt die situatie.

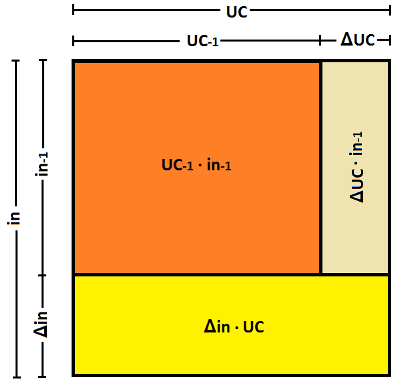
G&L merken op dat de laatste term in de voorgaande vergelijking, ΔUC · in_-1, staat voor de herwaardering van de uit de vorige periode overgebleven voorraad, als gevolg van de verandering van de prijs van de betreffende producten. Dit wordt in boekhoudkundige termen voorraadherwaardering (inventory valuation adjustment, IVA) genoemd.

Voorraadvorming

G&L veronderstellen vervolgens dat in elke periode een fractie ( 1 – σ ) van de verkochte producten s is gemaakt in de huidige periode en een fractie σ in de vorige periode:

            s = s · ( 1 – σ ) + s · σ

Dit betekent dus dat de voorraad aan het eind van de vorige periode gelijk is aan s · σ:

            in_-1 = s · σ

            σ = in_-1 / s

HWC nader bezien

Terug naar de historische loonkosten, HWC. Nogmaals de vergelijking voor HWC:

            HWC = ( WB – ΔIN )

G&L komen eerst met wat ze een intuïtieve definitie noemen van wat HWC betekent, namelijk de loonkosten van de goederen die in de huidige periode zijn verkocht. In dat geval moet gelden:

            HWC = s · σ · UC_-1 + s · ( 1– σ ) · UC

Waarin de eerste term staat voor het aantal in de lopende periode verkochte producten die zijn gemaakt in de vorige periode, s · σ, tegen de toen geldende loonkosten UC_-1, plus het aantal in de lopende periode gemaakte en verkochte producten, s · ( 1– σ ), maal de loonkosten in de lopende periode, UC. G&L merken op dat dit een intuïtieve definitie is, dus dat nog bewezen moet worden dat ze ook daadwerkelijk klopt. Met andere woorden, klopt het dat geldt:

( WB – ΔIN ) = s · σ · UC_-1 + s · ( 1– σ ) · UC ?

Hiervoor hebben we gezien dat ΔIN = Δin · UC + ΔUC · in_-1 en dat UC = WB / y. Die laatste vergelijking kunnen we herschrijven tot WB = UC · y. Als we die vergelijkingen voor ΔIN en voor WB invullen in het rechter deel van de voorgaande vergelijking, dan vinden we:

( WB – ΔIN ) = UC · y  – ( Δin · UC + ΔUC · in_-1)

Verder zagen we dat moet gelden dat Δin = in – in_-1 = y – s. Deze vergelijking kan worden herschreven tot y = s + in – in_-1 = s + Δin. Als we die laatste vergelijking voor y invullen in de vorige vergelijking dan vinden we (bedenk dat ΔUC = UC – UC_-1):

( WB – ΔIN )   = s · UC + Δin · UC – ( Δin · UC + ΔUC · in_-1)

                      = s · UC – ΔUC · in_-1

                               = s · UC – UC · in_-1 + UC_-1 · in_-1

                               = ( s – in_-1 ) · UC + UC_-1 · in_-1

Hiervoor zagen we dat in_-1 = s · σ. Als we dit invullen in de voorgaande vergelijking, dan vinden we:

         ( WB – ΔIN )   = ( s – s · σ) · UC + UC_-1 · s · σ

                              = ( 1 –σ ) · s · UC + s · σ · UC_-1

En daarmee is inderdaad gevonden wat we wilden aantonen, namelijk dat voornoemde intuïtieve definitie klopt en dat HWC staat voor de totale loonkosten van de goederen die in de huidige periode zijn verkocht. Op basis hiervan kan ook de vergelijking voor de historische kosten THC herschreven worden:

            THC = ( 1 –σ ) · s · UC + s · σ · UC_-1 + r_L-1 · IN_-1

En omdat geldt dat IN_-1 = in_-1 · UC_-1 en dat in_-1 = s · σ (zie hiervoor) volgt dat:

            THC     = ( 1 –σ ) · s · UC + s · σ · UC_-1 + r_L-1 · s · σ · UC_-1

                       = ( 1 –σ ) · s · UC + ( 1 + r_L-1 ) · s · σ · UC_-1

G&L introduceren op dit moment een derde nieuwe grootheid, historische eenheidskosten (HUC), die ze als volgt definiëren:

            HUC     = THC / s

                       = ( 1 –σ ) · UC + ( 1 + r_L-1 ) · σ · UC_-1

HUC staat daarmee voor de historische kosten per eenheid product.

 

Ondernemingswinsten als aandeel in de verkoopopbrengsten

G&L gaan verder om aan te tonen dat je de zo gedefinieerde ondernemingswinst kunt herschrijven tot een fractie van de verkopen. Ze stellen dat wat ze willen aantonen is dat “als prijzen een vaste verhouding hebben tot de historische productiekosten van de verkochte producten, dat de winsten dan in een constante verhouding zullen staan tot de opbrengsten van de verkopen in die periode”.

We zagen dat:

            F = S – ( WB – ΔIN ) – r_L-1 · IN_-1

            THC = ( WB – ΔIN ) + r_L-1 · IN_-1

Zodat:

            S = F + THC

Vervolgens stellen G&L dat je achteraf altijd kunt vaststellen dat de winst gelijk was aan een zekere fractie ϕ' (de zogenaamde mark-up, die hier met een toegevoegd aanhalingsteken ' om aan te geven dat ze achteraf wordt vastgesteld) van de totale historische kosten THC:

            F = ϕ' · THC

Combineer je dit met de vorige vergelijking, dan vind je:

            S = ( 1 + ϕ' ) · THC

Wat betekent dat:

            F / S     = ϕ' · THC / ( 1 + ϕ' ) · THC

                        = ϕ'  / ( 1 + ϕ' )

Terug naar de vergelijkingen THC = ( 1 –σ ) · s · UC + ( 1 + r_L-1 ) · s · σ · UC_-1 en S = ( 1 + ϕ' ) · THC. Als je in de laatste vergelijking THC vervangt door de eerste vergelijking, dan vind je:

            S = ( 1 + ϕ' ) · ( ( 1 –σ ) · s · UC + ( 1 + r_L-1 ) · s · σ · UC_-1 )

In het BMWK artikel was het prijsniveau p gedefinieerd als de opbrengsten per verkocht product:  p = S / s, zodat S = p · s. Bedenk verder dat we net zagen dat S = ( 1 + ϕ' ) · THC en dat HUC = THC / s zodat THC = HUC · s, wat betekent dat:

            S = ( 1 + ϕ' ) · THC

            p · s =  ( 1 + ϕ' ) · THC

            p · s =  ( 1 + ϕ' ) · HUC · s

            p = ( 1 + ϕ' )· HUC

Als je in deze laatste vergelijking invult dat HUC = ( 1 –σ ) · UC + ( 1 + r_L-1 ) · σ · UC_-1 zoals we hiervoor zagen, dan vind je:

            p = ( 1 + ϕ' ) · HUC

En dus:

            p = ( 1 + ϕ' ) · ( ( 1 –σ ) · UC + ( 1 + r_L-1 ) · σ · UC_-1 )

G&L merken op dat niet sterk genoeg kan worden onderstreept dat deze twee vergelijkingen niets meer zijn dan een definitie, een definitie die volgt uit de vaststelling achteraf dat de winst gelijk was aan een zekere fractie ϕ' van de totale historische kosten THC. Niettemin, zo stellen G&L, kun je er het nodige uit afleiden.

Zo kun je uit de een na laatste vergelijking aflezen dat als je een winstmarge zou willen nastreven die gelijk is aan ϕ' / ( 1 + ϕ' ), dat je dat kan bereiken door je verkoopprijzen gelijk te stellen aan een factor ϕ' / ( 1 + ϕ' ) maal de actuele waarde van HUC. G&L merken bij deze conclusie op dat later nog zal blijken dat dit in de praktijk niet helemaal zal lukken, maar dat ze heel dicht zal worden benaderd.

G&L stellen verder over deze vergelijking dat je er redelijk makkelijk actuele mark-ups mee kan berekenen, omdat er de nodige statistieken voorhanden zijn over bedrijfsverkopen en over bedrijfswinsten. Dat in tegenstelling tot vergelijkingen op basis van historische loonkosten, omdat die laatste alleen uit indirecte berekeningen kunnen worden afgeleid.

G&L stellen tenslotte dat de vergelijking moet opgaan, ongeacht de wijze waarop de prijsvorming tot stand komt. Ook als wordt aangenomen dat de prijsvorming zodanig tot stand komt dat de winstmarge steeds gelijk is aan het marginale product van kapitaal, moeten de prijzen op een zodanige manier bewegen alsof ze het gevolg zijn van een mark-up op de historische kosten.

 

Het onderscheid tussen bedrijfswinsten en kasstroom (cash flow)

In de voorgaande tekst zagen we dat de hoeveelheid geld die een ondernemer kan onttrekken aan zijn bedrijf en uitkeren als winst gelijk is aan de inkomsten uit de verkopen, minus de uitgaven aan lonen en rente, plus de verandering van de waarde van de voorraden:

            F = S – WB + ΔIN – r_L-1 · IN_-1

            F = S – THC

Maar kan hij dat geld ook zomaar onttrekken aan zijn bedrijf? Het antwoord is dat dit afhangt van de ontwikkeling van zijn voorraden. Als ΔIN positief is, dus als die voorraden zijn toegenomen, bestaat een deel van zijn winst uit die extra voorraden. De waarde van die extra voorraden kan hij niet als winst uitkeren, tenzij hij de productie ervan heeft gefinancierd met gekeend geld.

Hiermee zijn we aangekomen bij het belangrijke verschil tussen bedrijfswinst en cash flow (CF), de netto instroom van geld. Dat verschil bestaat, zo blijkt uit de voorgaande uitleg, uit de waardetoename van de voorraden:

CF = F - ΔIN

CF = S – WB – r_L-1 · IN_-1

G&L merken op dat dit onderscheid in de gangbare economische modellen niet wordt gemaakt, omdat in die modellen gemakshalve is verondersteld dat voorraden niet bestaan. Ze is niettemin zeer relevant omdat er situaties kunnen optreden waarin de waarde van de voorraden sterk kan veranderen. Uit de vergelijking ΔIN = Δin · UC + ΔUC · in_-1 die we hiervoor hebben afgeleid, kan worden afgelezen dat dit in twee situaties kan gebeuren:

• in situaties met hoge inflatie, waarin ΔUC snel stijgt;
  
• in situaties van snelle groei, waarin Δin snel stijgt.
  

In beide gevallen zal de winst die een bedrijf maakt een stuk groter zijn dan zijn cashflow, wat betekent dat ze het verschil, F – CF, alleen kan uitkeren aan haar aandeelhouders als ze dat verschil bijleent.

G&L merken op dat dit onderscheid tussen cash flow en winst goed helpt om de rol van kredietgeld in de economie uit te leggen. Zonder dat kredietgeld, die bankleningen, zou het voor bedrijven niet mogelijk zijn om al hun winst, of in geval van snelle groei of hoge inflatie zelfs maar een gedeelte van hun winst, als dividend uit te keren aan hun aandeelhouders.

 

De definitie van winst in de nationale rekening

G&L merken op dat de wijze van winstberekening zoals hiervoor aangegeven weliswaar wordt gebruikt door accountants van bedrijven, maar dat dit niet altijd wordt gedaan door de accountants van de overheid.

Als voorbeeld noemen G&L het Amerikaanse Bureau of Economic Analysis (BEA), die de zogenaamde National Income and Products Accounts (NIPA)  bijhoudt. Haar accountants berekenen de in de economie als geheel gegenereerde winst op een andere wijze. Hun berekeningswijze is gebaseerd op het gegeven dat het NIPA systeem van boekhouding uitgaat van het concept van productie.

Dat uitgangspunt komt erop neer dat het reële nationale inkomen (uitgedrukt in aantallen producten) gelijk moet blijven als de reële productie en de reële verkopen onveranderd blijven (ter herinnering, kleine letters geven reële waarden aan, hoofdletters geldwaarden):

            y = s + Δin

In de visie van de BEA-accountants is de nationale productie, even terug gaand naar het voorbeeld met de appels, gelijk aan het aantal geproduceerde appels. En dat aantal is weer gelijk aan het aantal verkochte appels (consumptie, c) plus het aantal onverkochte appels dat is toegevoegd aan de voorraad onverkochte appels (investering, i):

            y = c + i          

En zoals we eerder zagen kan deze vergelijking uitgedrukt in geld als volgt worden geschreven:

            Y = C + I = p · s + UC · Δin

NB. In deze vergelijking zijn de verkopen gewaardeerd op hun verkoopprijs p en is de toevoeging aan de voorraden gewaardeerd op haar actuele productieprijs UC, net als hiervoor steeds is gedaan en net als wordt gedaan door de NIPA-accountants.

Omdat geldt dat S = p · s en ΔIN = Δin · UC + ΔUC · in_-1, zodat Δin · UC = ΔIN – ΔUC · in_-1, kan de laatste vergelijking worden herschreven tot:

            Y = S + ΔIN – ΔUC · in_-1

Deze vergelijking verschilt op één punt van het inkomen van de bedrijven zoals dat uit de eerste tabel in dit artikel kan worden afgelezen. Dat verschil is de term ΔUC · in_-1, die door de BEA-accountants wordt aangeduid als stock appreciation (SA):

            SA = ΔUC · in_-1

Op basis van het voorgaande kan de winstvergelijking volgens de BEA-accountants als volgt worden geschreven:

            F_NIPA = S – WB + ΔIN – SA

Op basis van de voorgaande vergelijking en gelet op de vergelijking Y = S + ΔIN – SA geldt dat:

            F_NIPA = S – WB + ΔIN – SA

            F_NIPA = Y – WB

            Y = WB + F_NIPA

Met andere woorden, de nationale productie is gelijk aan de lonen plus de winsten op basis van de NIPA definitie. In jargon: de nationale productie is gelijk aan de som van de factor inkomsten lonen en winst.

G&L komen nu aan bij een nogal abstract punt. In mijn woorden komt dat punt erop neer dat de BEA-economen de term SA aftrekken van hun winstberekening, en dus van hun berekening van het nationale inkomen, omdat die niet te herleiden valt tot veranderingen in de reële productie. Zou de term SA wel meegenomen worden, dan zou dat bijvoorbeeld ingeval van inflatie leiden tot een overschatting van de actuele reële productie.

G&L stellen vervolgens dat de benadering van de BEA-accountants rammelt in twee opzichten. Ten eerste wijkt de NIPA-winst af van de definitie van winst als het bedrag dat kan worden uitgekeerd zonder de balans van bezittingen en verplichtingen van een bedrijf te verstoren. Maar belangrijker nog, de BEA-benadering is niet stock-flow consistent.

G&L merken op dat dit manco niet voorkomt in een andere belangrijke database van de Amerikaanse economie, de Flow of Funds Accounts (FOF), die wordt bijgehouden door de Amerikaanse centrale bank, de FED. In de FOF wordt de term SA (in de FOF aangeduid als IVA, inventory valuation adjustment) wel meegeteld in de winst, en vervolgens ook meegeteld in de investeringsuitgaven. Dit sluit aan bij de aanpak van G&L.

In het volgende artikel, Prijsvorming en de verdeling van het nationale inkomen, ga ik verder met het vervolg van hoofdstuk 8 van het boek van G&L, waarin ze nader ingaan op de prijsvorming door bedrijven en de consequenties daarvan voor de verdeling van het nationale inkomen over werknemers, ondernemers en kapitaalverschaffers.

© Anton van de Haar - oktober 2013