Vensim PLE is een computerprogramma om dynamische systemen te programmeren. Dat zijn systemen met onderdelen die zich in samenhang ontwikkelen in de tijd. Hoe dat werkt valt wellicht het beste uit te leggen met een simpel voorbeeld van een dynamisch systeem.
Lekkende waterton
Stel je voor dat je een waterton hebt, gevuld met water. Als je een gaatje in de bodem prikt, dan zal de ton leeglopen. In het begin gaat dat snel en daarna, naarmate het waterpeil in de ton daalt, gaat het steeds langzamer. Er is dus een verband tussen de hoeveelheid water in de ton en de snelheid waarmee het water eruit loopt.
De snelheid waarin de ton leegloopt, kun je aanduiden met St. Die zou je bijvoorbeeld kunnen uitdrukken in liters per seconde. De letter t staat voor de het tijdstip waarop je kijkt. Dat is van belang omdat S niet constant is maar afneemt naarmate de tijd vordert.
Als je goed kijkt naar die snelheid, dan zul je zien dat ze gelijk op gaat met het waterpeil in de ton. Dit peil noemen we Pt. Dat peil zou je kunnen uitdrukken in centimeters boven de bodem van de ton. Op het moment dat Pt gehalveerd is, is St ook gehalveerd. En op het moment dat Pt tot een tiende gezakt is, is St ook tot een tiende gezakt. Met andere woorden, St is evenredig met Pt :
St ≡ Pt
Dat betekent dat de verhouding tussen die twee, St / Pt steeds hetzelfde is, een constante dus. Als je die constante aangeeft met a, dan kun je schrijven:
St = a * Pt
Stel dat de ton een bodemoppervlakte heeft van 0,1 vierkante meter. Dat is 1.000 vierkante centimeter. Een daling van het waterpeil met 1 centimeter leidt dan tot een volumeafname van 1.000 kubieke centimeter, dus 1 liter per centimeter peildaling. Dat betekent dat er een relatie is tussen het volume aan water dat op een gegeven moment nog in de ton zit, Vt en de hoeveelheid water die er op dat moment uit stroomt, St:
Vt = 1 * Pt en dus St = a * Vt
We hebben dus een verband gevonden tussen de hoeveelheid water die op tijdstip t uit de ton stroomt en de hoeveelheid water die op dat tijdstip nog in de ton zit.
Integratie
Als je nu de ontwikkeling van V in de tijd wilt berekenen dan moet je twee dingen weten. Je moet allereerst weten hoeveel water er in de ton zat op het moment dat je hem lek prikte. Die hoeveelheid noemen we de beginwaarde, V0. Verder moet je van elk moment in de tijd weten hoeveel water er op dat moment is weggestroomd.
Nu komen we bij het enige lastige punt van Vensim. Om de op een gegeven tijdstip weggestroomde hoeveelheid water te kunnen bepalen moet je een integratie uitvoeren. In sommige gevallen kun je die integratie langs wiskundige weg afleiden, maar vaak lukt dat niet, dan moet je een benadering uitvoeren. Vensim gebruikt altijd die laatste optie.
Zo'n benadering is heel simpel en komt er op neer dat je het leeglopen van de ton in heel kleine stapjes knipt, bijvoorbeeld in stapjes van van een honderdste seconde. In die heel korte tijd zal de daling van Vt zo miniem zijn dat je Vt als constant mag veronderstellen. Dat betekent dat St dan ook constant is, want die is immers gelijk aan a * Vt. In elk stukje zal de afname van het volume dan gelijk zijn aan de tijdsduur van het stapje maal a maal de waarde van Vt in het begin van dat stapje. In een formule: 0,01 * a * Vt.
Een rekenvoorbeeld: stel dat er op tijdstip t nog 100 liter water in de ton zit en dat a gelijk is aan 0,001. Dat betekent dat St, de snelheid waarmee het water wegstroomt, dan gelijk aan a * Vt = 0,001 * 100 = 0,1 liter per seconde. De hoeveelheid water die in 0,01 seconde wegstroomt is dan gelijk aan 0,01 * St = 0,001 liter.
Als we nu de hoeveelheid water die in een zo'n stapje uit de ton stroomt ΔV noemen, dan krijgen we dus de volgende formule voor het eerste stapje (van t=0 seconden tot t = 0,01 seconden):
ΔV(t = 0,01) = 0,01 * a * V0
En in het tweede stapje (van t=0,01 seconden tot t = 0,02 seconden) wordt dan:
ΔV(t = 0,02) = 0,01 * a * (V0 - ΔV(t = 0,01))
Etc, etc, zodat je na heel veel stapjes bij het x-de stapje (van t= x * 0,01 - 0,01 seconden tot t=x * 0,01 seconden) het volgende krijgt:
ΔV(t = x * 0,01) = 0,01 * a * (V0 - ΔV(t = 0,01) - ΔV(t = 0,02) - ...... - ΔV(t = x * 0,01 ))
Als je het volume op een bepaald tijdstip wilt weten, dan moet je vervolgens van het volume V0 het volume aftrekken dat in alle tussenliggende stapjes is weggestroomd. Die benadering wordt beter naarmate de staafjes dunner en talrijker worden. Een schets van zo'n benadering is te zien in de volgende figuur.
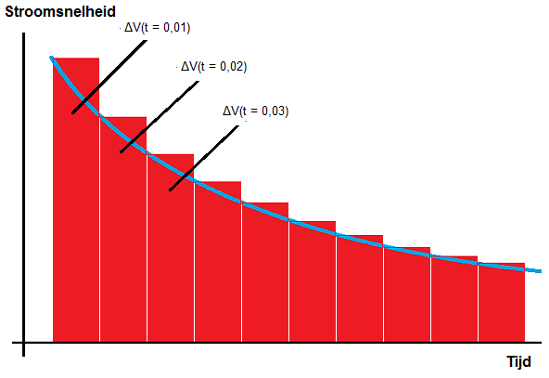
De blauwe lijn in de grafiek geeft de werkeliijke ontwikkeling weer van de stoomsnelheid in de tijd. De hoeveelheid water die werkelijk wegstroomt is gelijk aan het oppervlakte onder deze blauwe lijn. Maar de weggestroomde hoeveelheid water die we met de stapjesmethode berekenen is gelijk aan het opgetelde oppervlakte van alle rode staafjes. Je ziet dat de staafjesmethode in dit geval (bij een dalende lijn) een overschatting geeft van de hoeveelheid weggestroomd water, een overschatting die gelijk is aan de opgetelde oppervlakte van de rode driehoekjes boven de blauwe lijn. Stel je nu voor dat de staafjes veel smaller worden, dan zie je dat de opgetelde oppervlakte van de rode driehoekjes veel kleiner wordt. Dat is de essentie van de stapjes methode.
En dat is dus wat Vensim doet, ze rekent het systeem door in heel kleine stapjes (jargon: iteraties). Dat kost weliswaar heel veel rekenwerk, maar computers zijn tegenwoordig zo snel dat dit geen enkel probleem meer is.
Vensim PLE
In Vensim hoef je de integraties niet zelf uit te voeren, dat doet Vensim voor je, met de kleine stapjes methode die ik net heb beschreven. In Vensim kan je de leeglopende ton op de volgende manier programmeren:
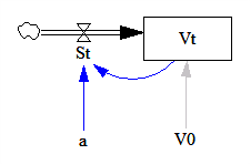
Het systeem heeft dezelfde variabelen die ik hiervoor al heb genoemd. V0 staat voor het volume aan water dat op het moment van lekprikken in de ton zat. Vt staat voor het volume dat er op enig moment nog in de ton zit. St staat voor de hoeveelheid water die er op enig moment uit stroomt. En a is de verhouding tussen St en Vt.
Vt is een zogenaamde stock variabele, een variabele die een voorraad aangeeft. Dat kan bijvoorbeeld een voorraad water in een ton of een hoeveelheid geld op een bankrekening zijn. Stock variabelen worden in Vensim altijd aangegeven met een boxje eromheen. Vensim noemt ze, om het ingewikkeld te maken, Box variabelen. Ik noem ze verder stock variabelen.
St is een zogenaamde flow variabele, een variabele die een stroom in de tijd aangeeft. Dat kan bijvoorbeeld een hoeveelheid water zijn die per seconde uit een waterton lekt of het maandelijkse inkomen van een werker of de hoeveelheid geld die per jaar in de economie omgaat (het GDP). Vensim noemt ze, om het ingewikkeld te maken, Rate variabelen. Ik noem ze verder flow variabelen. Ze worden altijd aangegeven met een wolkje van waaruit een pijl door een zandlopertje loopt.
De flow variabelen dienen naar een stock variabele te wijzen. De stock variabele is dan de integraal van de waarden die de flow variabele in de tijd aanneemt, net als hiervoor is uitgelegd. V0 en a tenslotte zijn van het type dat Vensim Variable - Auxilliary/constant noemt. Dat zijn alle overige variabelen. Ik noem ze verder overige variabelen.
In de figuur zijn een aantal blauwe en grijze pijltjes te zien. De blauwe pijltjes die van de ene variabele naar de andere wijzen betekenen dat de ene variabele gebruikt wordt bij de berekening van de andere. De grijze pijltjes wijzen altijd naar een stock variabele. De variabele van waaruit het grijze pijltje vertrekt wordt gebruikt als beginwaarde voor de integratie.
Als je in Vensim de variabelen aanklikt, dan kun je ze een bepaalde waarde geven of je kunt er een formule aan koppelen. Ik heb nu het volgende gedaan:
• V0: heb ik de waarde van 1.000 liter gegeven. Deze is aan Vt gekoppeld en wordt dus al beginwaarde voor de integratie gebruikt;
• a: heb ik de waarde 0,001 gegeven;
• St: heb ik de waarde Vt * a gegeven (daarom wijzen er blauwe pijltjes van Vt en van a naar St);
• Vt: heb ik de waarde –St gegeven (daarom wijst er een blauw pijltje van St naar Vt). Dat betekent dat Vt begint bij V0, dus bij 1.000 liter en dan daalt omdat er bij elk ministapje opnieuw de waarde – St * Δt van wordt afgetrokken. Vensim vermenigvuldigt bij die integratie automatisch -St met de grootte van de stapjes die ze gebruikt. Vt geeft dus de hoeveelheid water aan die er naarmate de tijd verstrijkt nog in de ton zit.
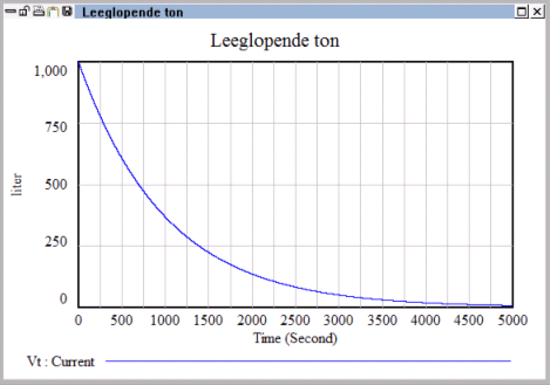
Het programmeren van dit systeempje in Vensim kost je hooguit een paar minuten. In de volgende figuur, gemaakt door Vensim, is waarde van Vt in de tijd aangegeven.
Overigens hoef je in Vensim voor het aangeven van een stroom in de tijd niet per se een flow variabele te gebruiken. Je kunt ook een overige variabele gebruiken. Het onderscheid tussen flow variabelen en overige variabelen maakt Vensim alleen maar om duidelijk weer te geven wat er gebeurt. Als je voor St een overige variabele gebruikt, dan ziet het er op het scherm zo uit:
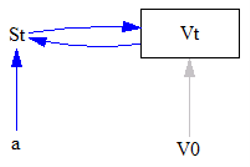
De waarden van de variabelen zijn precies hetzelfde gebleven als hiervoor en het resultaat is ook precies hetzelfde. Het voordeel van de laatste methode is simpel, het kost minder ruimte op het scherm om hetzelfde systeem weer te geven. Dat is handig voor het overzicht als je complexere systemen programmeert.
Chaotisch gedrag
Het voorgaande voorbeeld van een leeglopende waterton is een mooi voorbeeld van een systeem dat zich op een eenduidige wijze ontwikkelt. Systemen, ook eenvoudige, hoeven zich echter lang niet altijd zo simpel te ontwikkelen. Een mooi voorbeeld is het al eerder genoemde Lorenz systeem. Dat is een systeem dat de convectie in de atmosfeer beschrijft. In Vensim PLE geprogrammeerd ziet het er als volgt uit.
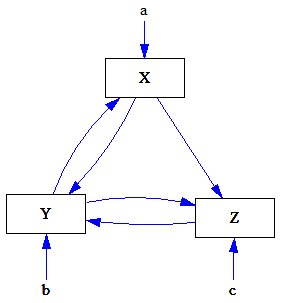
In dit systeem zijn X, Y en Z stock variabelen en a, b en c constanten. De formules voor de verandering van X, Y en Z in de tijd zijn als volgt:
ΔX/Δt = a * ( X - Y)
ΔY/Δt = X * ( b -Z )
ΔZ/Δt = X * Y - c * Z
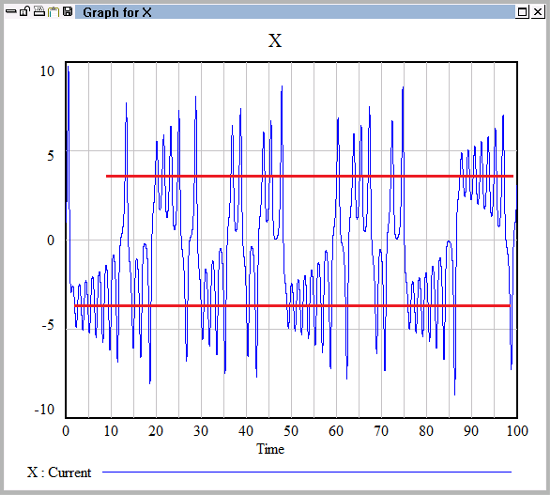
Het gaat veel te ver om uit te leggen wat deze formules precies betekenen (en eerlijk gezegd weet ik het zelf ook niet precies). Waar het nu even om gaat is dat de variabelen X, Y en Z zich in de tijd op chaotische wijze kunnen ontwikkelen. In het volgende plaatje is de ontwikkeling van X aangegeven voor bepaalde waarden van a, b en c en bepaalde beginwaarden voor X, Y en Z. De rode lijnen heb ik toegevoegd. Dat zijn niveau's waaromheen X "graag" op en neer veert. Dergelijke niveau's worden in jargon strange attractors genoemd.
In het plaatje hieronder is X tegen Z uitgezet. De blauwe lijn geeft de ontwikkeling van X en Z samen in de tijd weer. Als je dit plaatje met het voorgaande plaatje vergelijkt dan zie je dat de twee holtes in het onderstaande plaatje overeenkomen met posities van de rode lijnen, de strange attractors in het vorige plaatje. En nu begrijp je ook gelijk waar de term vlindereffect eigenlijk vandaan komt...
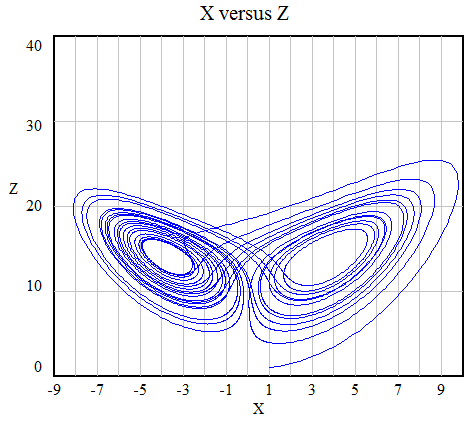
Een kenmerk van het Lorenz systeem is dat het nooit een evenwicht bereikt, het blijft altijd "slingeren". Net als ons vele malen ingewikkeldere economische systeem.
Download en handleidingen
Vensim PLE kan gratis worden gedownload van de website van de ontwikkelaar, Ventana Systems. Het adres is http://www.vensim.com/freedownload.html
Op het internet circuleren verschillende beknopte handleidingen van Vensim. Als je googeld op de volgende trefwoorden, dan vind je ze vanzelf:
• Princeton Vensim PLE Tutorial 1
• Princeton Vensim Tutorial 2
• Kirkwood Vensim PLE Quick Reference and Tutorial
In het volgende artikel heb ik Steve Keen’s Endogeen geld model uitgewerkt in Vensim.
© Anton van de Haar - september 2012